本文引用自文献:1)《大话数据结构》作者:程杰;
图的定义
在线性表中,数据元素之间是被串起来的,仅有线性关系,每个数据元素只有一个直接前驱和一个直接后继。在树形结构中,数据元素之间有着明显的层次关系,并且每一层上的数据元素可能和下一层中多个元素相关,但只能和上一层中的一个元素相关。而图这种数据结构比线性表和树要更加复杂,如下图所示。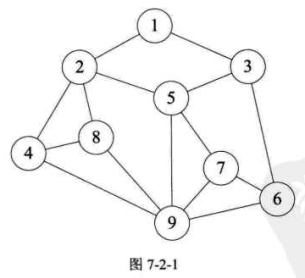
图的定义:
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:$G(V,E)$,其中,$G$表示一个图,$V$是图$G$中顶点的集合,$E$是图$G$中边的集合。
对于图的定义,有几点需要额外说明一下:
- 线性表中我们把数据元素叫做元素,树中将数据元素叫结点,在图中,数据元素我们称之为顶点(Vertex)。
- 线性表中可以没有数据元素,称为空表。树中没有可以没有结点,叫做空树。但对于图中则不能没有顶点,在图的定义中,强调了顶点集合V是有穷非空的。
- 线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻两层的结点具有层次关系,而图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
有向图和无向图
无向边:若顶点$v_i$到$v_j$之间的边没有方向,则称这条边为无向边,用无序偶对$(v_i,v_j)$来表示。如果图中任意两个顶点之间的边都是无向边,则称改图为无向图(Undirected Graphs)。图7-2-2就是一个无向图,由于边是无方向的,连接顶点A和D的边,可以表示成无序对$(A,D)$,也可以写成$(D,A)$。对于图7-2-2中的无向图$G_1$来说,$G_1=(V_1,\lbrace E_1 \rbrace)$,其中顶点集合$V_1=\lbrace A,B,C,D \rbrace$;边集合$E_1=\lbrace(A,B),(B,C),(C,D),(D,A),(A,C)\rbrace$。
有向边:若从顶点$v_i$到$v_j$的边有方向,则称这条边为有向边,也称为弧(Arc)。用有序偶对$\langle v_i,v_j \rangle$来表示。$v_i$称为弧尾(Tail),$v_j$称为弧头(Head)。如果图中任意两个顶点之间的边都是有向边,则称该图为有向图(Directed Graphs)。图7-2-3就是一个有向图。连接顶点A到D的有向边就是弧,A是弧尾,D是弧头,$\langle A,D \rangle$表示弧,注意不能写成$\langle D,A \rangle$。
对于图7-2-3中的有向图$G_2$来说,$G_2=(V_2,\lbrace E_2 \rbrace)$,其中顶点集合$V_2=\lbrace A,B,C,D \rbrace$;边集合$E_2=\lbrace \langle A,D \rangle,\langle B,A \rangle,\langle C,A \rangle,\langle B,C \rangle \rbrace$。
注意:无向边是小括号“$()$”表示,而有向边则是用尖括号“$\langle\rangle$”表示。
网(网络)
有些图的边或弧具有与他相关的数字,这种与图的边或弧相关的数叫做权(Weight)。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网(Network)。
图7-2-3就是一张带权的图,即标识中国四大城市的直线距离的网,此图中的权就是两地的距离。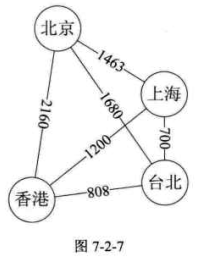
子图
假设有两个图$G= (V,\lbrace E \rbrace)$和$G’= (V’,\lbrace E’ \rbrace)$,如果$V’$是$V$的子集(即$V’ \subseteq V$),且$E’$是$E$的子集(即$E’ \subseteq E$),则称$G’$为$G$的子图。如下图7-2-8带底纹的图均为左侧无向图与有向图的子图。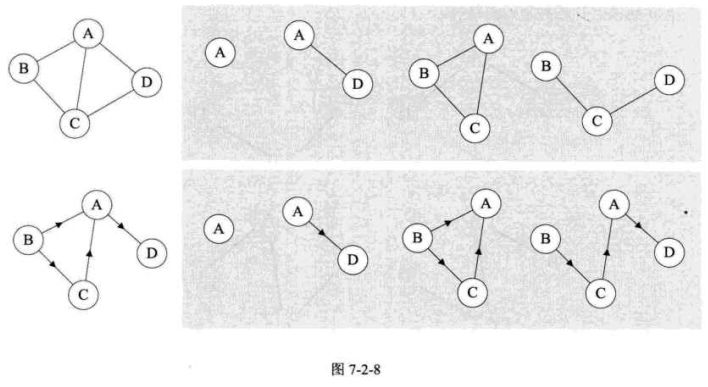
度
无向图的度
对于无向图$G= (V,\lbrace E \rbrace)$, 如果边$(v,v’)$属于$E$(即$(v,v’) \in E$), 则称顶点$v$和$v’$互为邻接点,即$v$和$v’$相邻接、边$(v,v’)$依附于顶点$v$和$v’$,或者说$(v,v’)$与顶点$v$和$v’$相关联。
顶点$v$的度是和$v$相关联的边的数目,记为$TD(v)$。
例如图7-2-8左侧上方的无向图,顶点$A$与$B$互为邻接点,边$(A,B)$依附于顶点$A$与$B$上,顶点$A$的度为3。而此图的边数是5,各个顶点度的和=3+2+3+2=10,推敲后发现,边数其实就是各顶点度数和的一半,多出的一半是因为重复两次计数。得出公式,$e=1/2\sum_{i=1}^nTD(v_i)$。
有向图的度
对于有向图$G= (V,\lbrace E \rbrace)$, 如果弧$\langle v,v’ \rangle$属于$E$(即$\langle v,v’ \rangle \in E$), 则称顶点$v$邻接到顶点$v’$互为邻接点,顶点$v’$邻接自$v$。弧$\langle v,v’ \rangle$和顶点$v$、$v’$相关联。
以顶点$v$为头的弧的数目称为$v$的入度(InDegree),记为$ID(v)$;以$v$为尾的弧的数目称为$v$的出度(OutDegree),记为$OD(v)$;顶点$v$的度$TD(v)=ID(v)+OD(v)$。
例如图7-2-8左侧下方的有向图,顶点$A$的入度是2(从$B$到$A$的弧,从$C$到$A$的弧),出度是1(从$A$到$D$的弧),所以顶点A的度为2+1=3。此有向图的弧有4条,而各顶点的出度和=1+2+1+0=4,各顶点的入读和=2+0+1+1=4。所以得到公式:$e=\sum_{i=1}^nID(v_i)=\sum_{i=1}^nOD(v_i)$。