本文引用自文献:1)《大话数据结构》作者:程杰;
二叉树的存储结构
二叉树顺序存储结构
前面我们已经谈到了树的存储结构,并且谈到顺序存储对树这种一对多的关系结构实现起来是比较困难的。但是二叉树是一种特殊的树,由于它的特殊性,使得用顺序存储结构也可以实现。
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲和孩子的关系,左右兄弟的关系等。
先来看看完全二叉树的顺序存储,一棵完全二叉树如图6-7-1所示。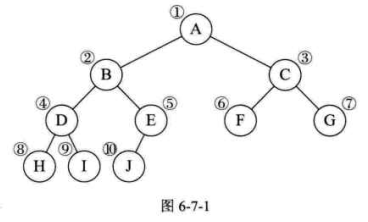
将这棵二叉树存入到数组中,相应的下标对应其同样的位置,如图6-7-2所示。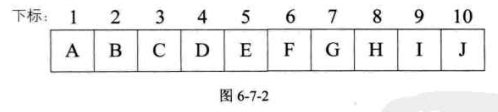
这下可以看出完全二叉树的优越性来了吧。由于它定义的严格,所以用顺序结构也可以表现出二叉树的结构来。
当然对于一般的二叉树,尽管层序编号不能反映逻辑关系,但是可以将其按完全二叉树编号,只不过,把不存在的结点设置为“∧”而已。如图6-7-3,注意浅色结点表示不存在。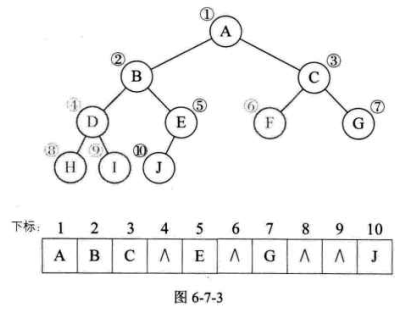
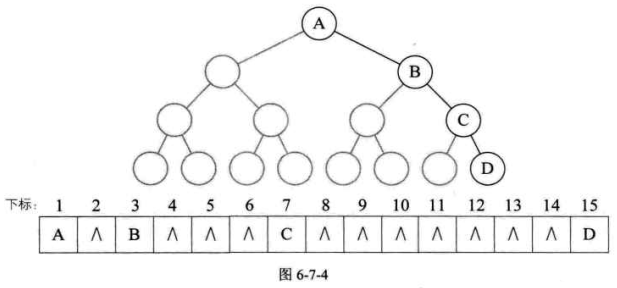
考虑一种极端的情况,一棵深度为k的右斜树,它只有k个结点,确需要分配$2^k-1$个存储单元空间,这显然是对存储空间的浪费,如图6-7-4所示。所以,顺序存储结构一般只用于完全二叉树。
二叉链表
既然顺序存储适用型不强,我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。用Java代码可以定义如下。1
2
3
4
5
6
7
8
9
10
11
12/**
* 二叉树的二叉链表结点结构
*/
class BiTNode<T> {
/* 节点数据 */
private T data;
/* 左右孩子指针 */
private BiTNode lchild, rchild;
}
结构示意图如图6-7-5所示。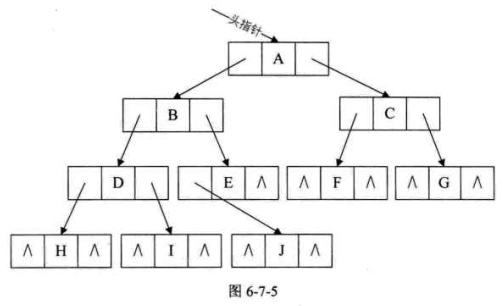
就如同树的存储结构中讨论的一样,如果有需要,还可以再增加一个指向其双亲的指针域,那样就称之为三叉链表。由于与树的存储结构类似,这里就不详述了。
遍历二叉树
二叉树遍历原理
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
这里有两个关键词:访问和次序。
访问其实是要根据实际的需要来确定具体做什么,比如对每个结点进行相关计算,输出打印等,它算是一个抽象操作。在这里我们可以简单地假定就是输出节点的数据信息。
二叉树的遍历次序不同于线性结构,线性结构最多也就是从头至尾、循环、双向等简单的遍历方式。树的结点之间不存在唯一的前驱和后继关系,在访问一个结点后,下一个被访问的结点可以有不同的选择。
二叉树遍历方法
二叉树的遍历方法可以很多,如果我们限制了从左到右的习惯方式,那么就要就分为四种:
前序遍历
规则是若二叉树为空,则空操作返回否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。如图6-8-2所示,遍历的顺序为:ABDGHCEIF。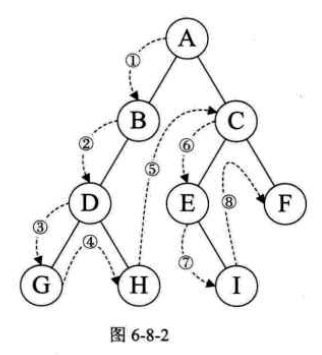
中序遍历
规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后访问根结点,最后中序遍历右子树。如图6-8-3所示,遍历的顺序为:GDHBAEICF。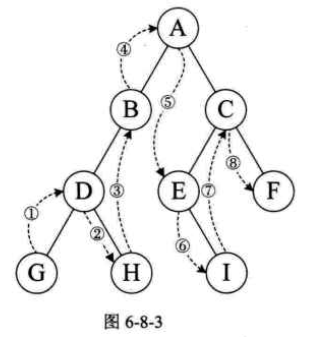
后序遍历
规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点。如图6-8-4所示,遍历的顺序为:GHDBIEFCA。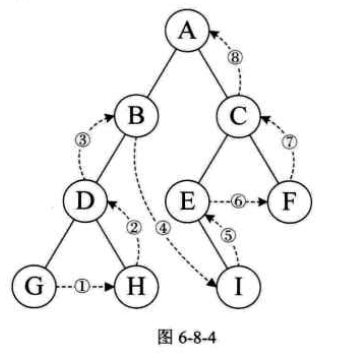
层序遍历
规则是若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对节点逐个访问。如图6-8-5所示,遍历的循序为:ABCDEFGHI。
有同学会说,研究这么多遍历的方法干什么呢?
我们用图形的方式来表现树的结构,应该说是非常直观和容易理解,但是对于计算机来说,它只是循环、判断等方式来处理,也就是说,它只会处理线性序列,而我们刚才提到的四种遍历方法,其实都是把在树中的 结点变成某种意义的线性序列,这就给程序的实现带来了好处。
另外不同的遍历提供了对结点依次处理的不同方式,可以在遍历过程中对结点进行各种处理。
前序遍历算法
二叉树的定义是用递归的方式,所以实现遍历算法也可以采用递归,而且极其简洁明了。先来看看二叉树的前序遍历算法,代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13/**
* 二叉树的前序遍历递归算法
*
* @param root
*/
public void preOrderTraverse(BiTNode root) {
if (root == null) {
return;
}
System.out.println(root.getData()); //访问节点
preOrderTraverse(root.getLchild()); //再先序遍历左子树
preOrderTraverse(root.getRchild()); //最后先序遍历右子树
}
中序遍历算法
那么二叉树的中序遍历算法是如何呢?别以为很复杂,它和前序遍历算法仅仅只是代码的顺序上的差异。1
2
3
4
5
6
7
8
9
10
11
12
13/**
* 二叉树的中序遍历递归算法
*
* @param root
*/
public void inOrderTraverse(BiTNode root) {
if (root == null) {
return;
}
inOrderTraverse(root.getLchild()); //中序遍历左子树
System.out.println(root.getData()); //访问节点
inOrderTraverse(root.getRchild()); //最后中序遍历右子树
}
换句话说,它等于是把调用左孩子的递归函数提前了,就这么简单。
后续遍历算法
那么同样的,后序遍历算法也就很容易想到应该如何写代码了。1
2
3
4
5
6
7
8
9
10
11
12
13/**
* 二叉树的后序遍历递归算法
*
* @param root
*/
public void postOrderTraverse(BiTNode root) {
if (root == null) {
return;
}
postOrderTraverse(root.getLchild()); //先后序遍历左子树
postOrderTraverse(root.getRchild()); //再后序遍历右子树
System.out.println(root.getData()); //访问节点
}
层序遍历算法
层序遍历算法有点不一样,可以用一个队列Queue,初始先把root结点加入到队列,然后从队列中获取结点,并且如果获取到的结点的左右孩子不为空将左右孩子加入到队列中即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public static void layerOrderTraverse(BiTNode root){
if(root == null){
return;
}
//层序遍历
Queue<BiTNode> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
BiTNode node = queue.poll();
System.out.print(node.getData());
BiTNode lchild = node.getLchild();
if(lchild != null){
queue.add(lchild);
}
BiTNode rchild = node.getRchild();
if(rchild != null){
queue.add(rchild);
}
}
}
推导遍历结果
有一种题目为了考查对二叉树遍历的掌握程度,是这样出题的。一直一颗二叉树的前序遍历序列为$ABCDEF$,中旭遍历序列为$CBAEDF$,请问这棵二叉树的后序遍历结果是多少?
我们知道,三种遍历都是从根结点开始,前序遍历是先打印在递归左和右。所以前序遍历序列为$\underline{A}BCDEF$,第一个字母$A$被打印出来,就说明$A$是根结点的数据。再由中序遍历序列是$CB\underline{A}EDF$,可以知道$C$和$B$是$A$的左子树的结点,$E$、$D$、$F$是$A$的右子树的结点,如图6-8-21所示。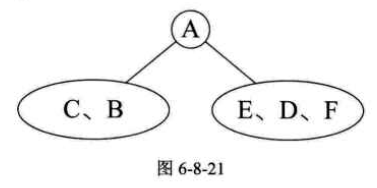
然后我们看前序中的$C$和$B$,它的顺序是$A\underline{BC}DEF$,是先打印$B$后打印$C$,所以$B$应该是$A$的左孩子,而$C$就只能是$B$的孩子,此时是左还是右孩子还不确定。在看中序序列是$\underline{CB}AEDF$,$C$是在$B$的前面打印,这就说明$C$是$B$的左孩子,如图6-8-22所示。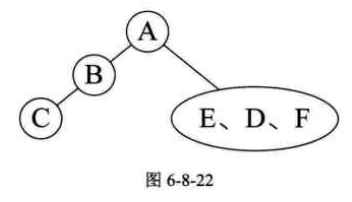
再看前序中的$E$、$D$、$F$,它的顺序是$ABC\underline{DEF}$,那就意味着$D$是$A$结点的右孩子,$E$和$F$是$D$的子孙,注意,它们中有一个不一定是孩子,还有可能是孙子的。再来看中序序列是$CBA\underline{EDF}$,由于$E$的$D$的左侧,而$F$在右侧,所以可以确定$E$是$D$的左孩子,$F$是$D$的右孩子。因此最终得到的二叉树是图6-8-23所示。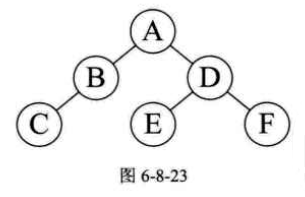
至此,想要得到后序遍历序列就很简答了,结果是$CBEFDA$。
但其实,如果足够熟练,不用画这棵二叉树,也可以得到后序的结果。因为刚才判断了$A$结点是跟结点,那么它在后序序列中,一定是最后一个。刚才推导出$C$是$B$的左孩子,而$B$是$A$的左孩子,那就意味着后序序列的前两位一定是$CB$。同样的办法也可以得到$EFD$的后序顺序,最终就得到$CBEFDA$的结果。
二叉树遍历的重要性质
二叉树遍历有两个重要性质:
- 已知前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
- 已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
但是注意,已知前序和后序遍历,是不能确定一棵二叉树的,原因也很简单,比如前序序列是$ABC$,后序序列是$CBA$。我们可以确定$A$一定是根结点,但接下来,我们无法知道,哪个结点是左子树,哪个是右子树。这棵树可能有如图6-8-24所示的四种可能。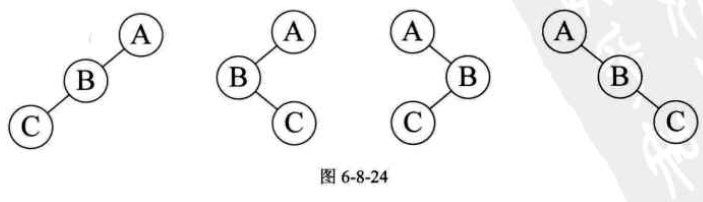
二叉树的建立
上面我们提到根据前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。那么我们根据前序遍历序列和中序遍历序列就可以创建一棵唯一的二叉树出来,具体代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35/**
* 创建一棵二叉树
*
* @param preOrder 二叉树的先序序列
* @param inOrder 二叉树的中序序列
* @return 返回二叉树的根结点
*/
public static <E> BiTNode<E> buildTree(E[] preOrder, E[] inOrder) {
if (preOrder == null || preOrder.length == 0) {
return null;
}
BiTNode<E> root = new BiTNode<>(preOrder[0]);
//找到inOrder中的root的位置
int inOrderIndex = 0;
for (char i = 0; i < inOrder.length; i++) {
if (inOrder[i] == root.getData()) {
inOrderIndex = i;
}
}
//preOrder的左子树和右子树部分
E[] preOrderLeft = Arrays.copyOfRange(preOrder, 1, 1 + inOrderIndex);
E[] preOrderRight = Arrays.copyOfRange(preOrder, 1 + inOrderIndex, preOrder.length);
//inOrder的左子树和右子树部分
E[] inOrderLeft = Arrays.copyOfRange(inOrder, 0, inOrderIndex);
E[] inOrderRight = Arrays.copyOfRange(inOrder, inOrderIndex + 1, inOrder.length);
//递归建立左子树和右子树
BiTNode leftChild = buildTree(preOrderLeft, inOrderLeft);
BiTNode rightChild = buildTree(preOrderRight, inOrderRight);
root.setLchild(leftChild);
root.setRchild(rightChild);
return root;
}
当然,根据后序遍历序列和中序遍历序列也一样可以创建出一棵二叉树,代码逻辑是类似的。