本文引用自文献:1)《大话数据结构》作者:程杰;
二叉树的定义
二叉树(Binary Tree)是n(n >= 0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两颗互不相交的、分别称为根结点的左子树和右子树的二叉树组成。如下图就是一颗二叉树。
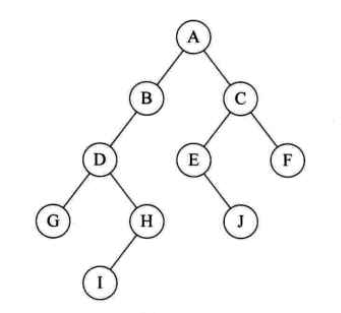
二叉树的特点
二叉树的特点有:
- 每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点。注意不是有两棵子树,而是最多有两棵,没有子树或者有一棵子树都是可以的。
- 左子树和右子树是有顺序的,次序不能任意颠倒。就像人是双手、双脚,但显然左手、左脚和右手、右脚是不一样的。
- 即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。下图中树1和树2是同一棵树,但它们确实不同的二叉树。
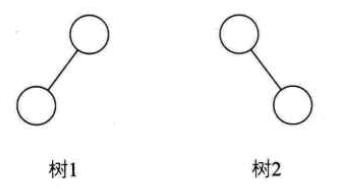
特殊二叉树
斜树
顾名思义,斜树一定要是斜的,但是往哪斜还是有讲究。所有的结点都只是左子树的二叉树叫左斜树,所有结点都是只有右子树的二叉树叫右斜树,这两者统称为斜树。下图中就是左斜树和右斜树。斜树有很明显的特点,就是每一层都只有一个结点,结点的个数与二叉树的深度相同。
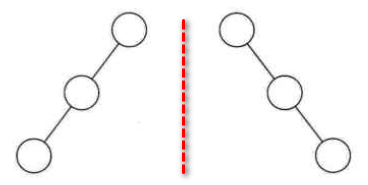
有人可能想,斜树看上去不就和线性表结构一样的吗?确实,其实线性表就可以理解为树的一种极其特殊的表现形式。
满二叉树
在一棵二叉树中,如果所有的分支节点都存在左子树和右子树,并且所有的叶子结点都在同一层上,这样的二叉树称为满二叉树。
下图就是一棵满二叉树,从样子上看起来就很完美。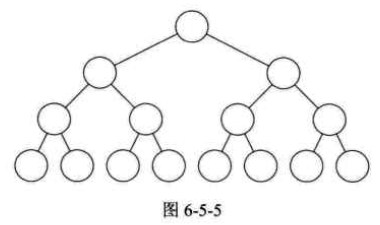
满二叉树的特点有:
- 叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
- 非叶子结点的度一定是2。否则就是“缺胳膊少腿”了。
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子树最多。
完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1 <= i <= n)的结点与同样深度的满二叉树编号为i的结点在二叉树中位置完全相同,则这颗二叉树称为完全二叉树,如下图所示。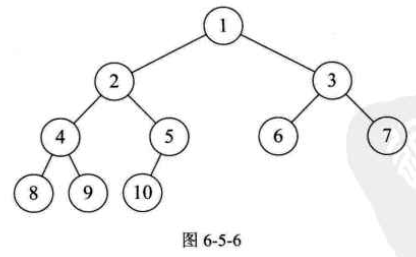
这是一种有些理解难度的特殊二叉树。
首先从字面上要区分,“完全”和“满”的差异,满二叉树一定是一棵完全二叉树,但完全二叉树不一定的满的。
其次,完全二叉树的所有结点和同样深度的满二叉树,它们按层序编号相同的结点,是一一对应的。这里有个关键词是按层序编号,像下图中的树1,因为5节点没有左子树,却有右子树,那就使得按层序编号的第10个编号空挡了。同样道理,树2中由于3结点没有子树,所以使得6、7编号的位置空挡了。树3又是因为5编号下没有子树造成第10和第11位置空挡,只有上图6-5-6中的树,尽管它不是满二叉树,但是编号是连续的,所以它是完全二叉树。
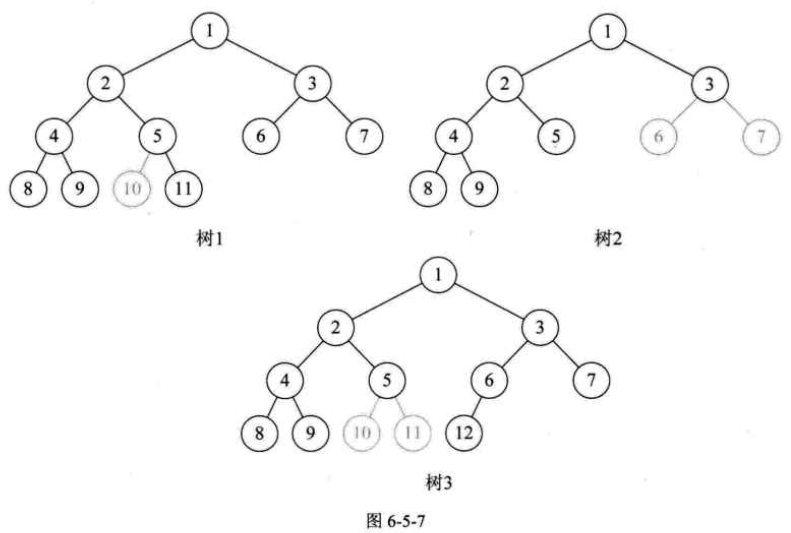
二叉树的一些特点:
- 叶子结点只能出现在最下两层。
- 最下层的叶子一定集中在左部连续位置。
- 倒数第二鞥,若有叶子结点,一定都是右部连续位置。
- 如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况。
- 同样结点树的二叉树,完全二叉树的深度最小。
从上面的例子,也给了我们一个判断某二叉树是否是完全二叉树的办法,那就是看着树的示意图,心中默默给每个结点按照满二叉树的结构逐层顺序编号,如果编号出现空挡,就说明不是完全二叉树,否则就是。
二叉树的性质
二叉树有一些需要理解并记住的特性,以便于我们更好地使用它。
二叉树的性质1
性质1:在二叉树的第i层至多有$2^{i-1}$个结点(i>=1)。
这个性质很好记忆,观察一下图6-5-5。
第一层是根结点,只有一个,所以$2^{1-1}=2^0=1$。
第二层有两个,$2^{2-1}=2^1=2$。
第三层有四个,$2^{3-1}=2^2=4$。
第四层有八个,$2^{4-1}=2^3=8$。
通过数学归纳法的论证,可以很容易得出在二叉树的第i层上至多有$2^{i-1}$个结点(i>=1)的结论。
二叉树的性质2
性质2:深度为k的二叉树至多有$2^k-1$个结点(k>=1)。。
注意这里一定要看清楚,是$2^k$后再减去1,而不是$2^{k-1}$。
深度为k意思就是有k层的二叉树,我们先来看看简单的。
如果有一层,至多有$1=2^1-1$个结点。
如果有两层,至多有$1+2=3=2^2-1$个结点。
如果有三层,至多有$1+2+4=7=2^3-1$个结点。
如果有四层,至多有$1+2+4+8=15=2^4-1$个结点。
通过数据归纳法的论证,可以得出,如果有k层,此二叉树至多有$2^k-1$个结点。
二叉树的性质3
性质3:对任何一棵二叉树T,如果其终端结点数为$n_0$,度为2的节点数为$n_2$,则$n_0=n_2+1$。
终端结点数其实就是叶子结点数,而一棵二叉树,除了叶子结点外,剩下的就是度为1或2的节点数了,我们设$n_1$为度是1的结点数。则树T结点总数$n=n_0+n_1+n_2$。
比如图6-6-1的例子,结点总数为10,它是由A、B、C、D等度为2的结点,F、G、H、I、J等度为0的叶子结点和E这个度为1的结点组成。总和为4+1+5=10。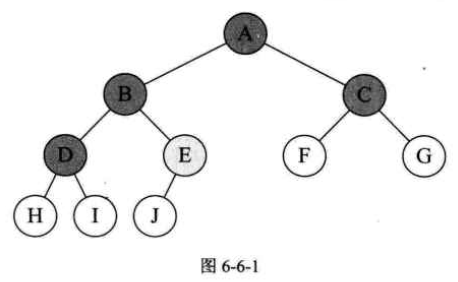
我们换个角度,再数一数它的连接线数,由于根结点只有分支出去,没有分支进来,所以分支线总数为节点总数减1。图6-6-1就是9个分支。对于A、B、C、D结点来说,它们都有两个分支线出去,而E结点只有一个分支线出去。所以总分支线为$4×2+1×1=9$。
用代数表达就是$分支线总数=n-1=n_1+2n_2$。因为刚才我们有等式$n=n_0+n_1+n_2$,所以可推导出$n_0+n_1+n_2-1=n_1+2n_2$。结论就是$n_0=n_2+1$。
二叉树的性质4
性质4:具有n个结点的完全二叉树的深度为$\lfloor log_2 n \rfloor + 1$($\lfloor x \rfloor$表示不大于x的最大整数,即向下取整)。
由满二叉树的定义我们可以知道,深度为k的满二叉树的节点树h一定是$2^k - 1$。因为这是最多的节点个数,那么对于$n=2^k - 1$倒推得到满二叉树的度为$k=log_2 (n+1)$,比如结点数为15的满二叉树,度为4。
完全二叉树我们前面已经提到,它是一颗具有n个结点的二叉树,若按层序编号后其编号与同样深度的满二叉树中编号结点在二叉树中位置完全相同,那它就是完全二叉树。也就是说,它的叶子结点只会出现在最下面的两层。
它的结点数一定少于等于同样度数的满二叉树的结点数$2^k-1$,但一定多余$2^{k-1}-1$,即满足$2^{k-1}-1<n<=2^k-1$。由于结点数n是整数,$n<=2^k-1$意味着$n<2^k$,$n>2^{k-1}-1$意味着$n>=2^{k-1}$,所以$2^{k-1}<=n<2^k$,不等式两边取对数,得到$k-1<=log_2 n<k$,而k作为度数也是整数,因此$k=\lfloor log_2 n \rfloor + 1$。
二叉树的性质5
性质5:如果对一棵有n个结点的完全二叉树(其深度为$\lfloor log_2 n \rfloor + 1$)的结点按层序编号(从第一层到第$\lfloor log_2 n \rfloor + 1$),每层从左到右),对任一结点i(1<=i<=n)有:
- 如果i=1,则节点i是二叉树的根,无双亲;如果i>1,则其双亲是结点$\lfloor i/2 \rfloor$。
- 如果$2i>n$,则结点无左孩子(节点i为叶子结点);否则其左孩子是结点$2i$。
- 如果$2i+1>n$,则结点i无右孩子;否则其右孩子是结点$2i+1$。
我们以图6-6-2为例,来理解这个性质。这是一棵完全二叉树,度为4,结点总数是10。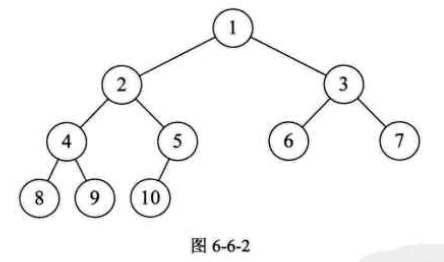
对于第一条来说是很显然的,$i=1$时就是根结点。$i>1$时,比如结点7,它的双亲就是$\lfloor 7/2 \rfloor=3$,节点9,它的双亲就是$\lfloor 9/2 \rfloor=4$。
第二条,比如结点6,因为$2×6=12$超过了结点总数10,所以结点6无左孩子,它是叶子结点。同样,而结点5,因为$2×5=10$正好是结点总数10,所以它的左孩子是结点10。
第三条,比如结点5,因为$2×5+1=11$,大于结点总数10,所以它无右孩子。而结点3,因为$2×3+1=7$小于10,所以它的右孩子是结点7。