归并排序和快速排序的时间复杂度比冒泡、插入这种简单的排序要好,都是O(nlogn)。
归并排序
归并排序(Merge-Sort)是利用归并思想实现的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案”修补”在一起,即分而治之。
分治过程分析
归并排序的过程分为“分”和“治”,其大致过程是采用二分的方式,使最小的子序列有序,然后从最小的子序列开始合并,得到次小的有序子序列,以此类推,最后得到完全有序的序列。
画图说明如下。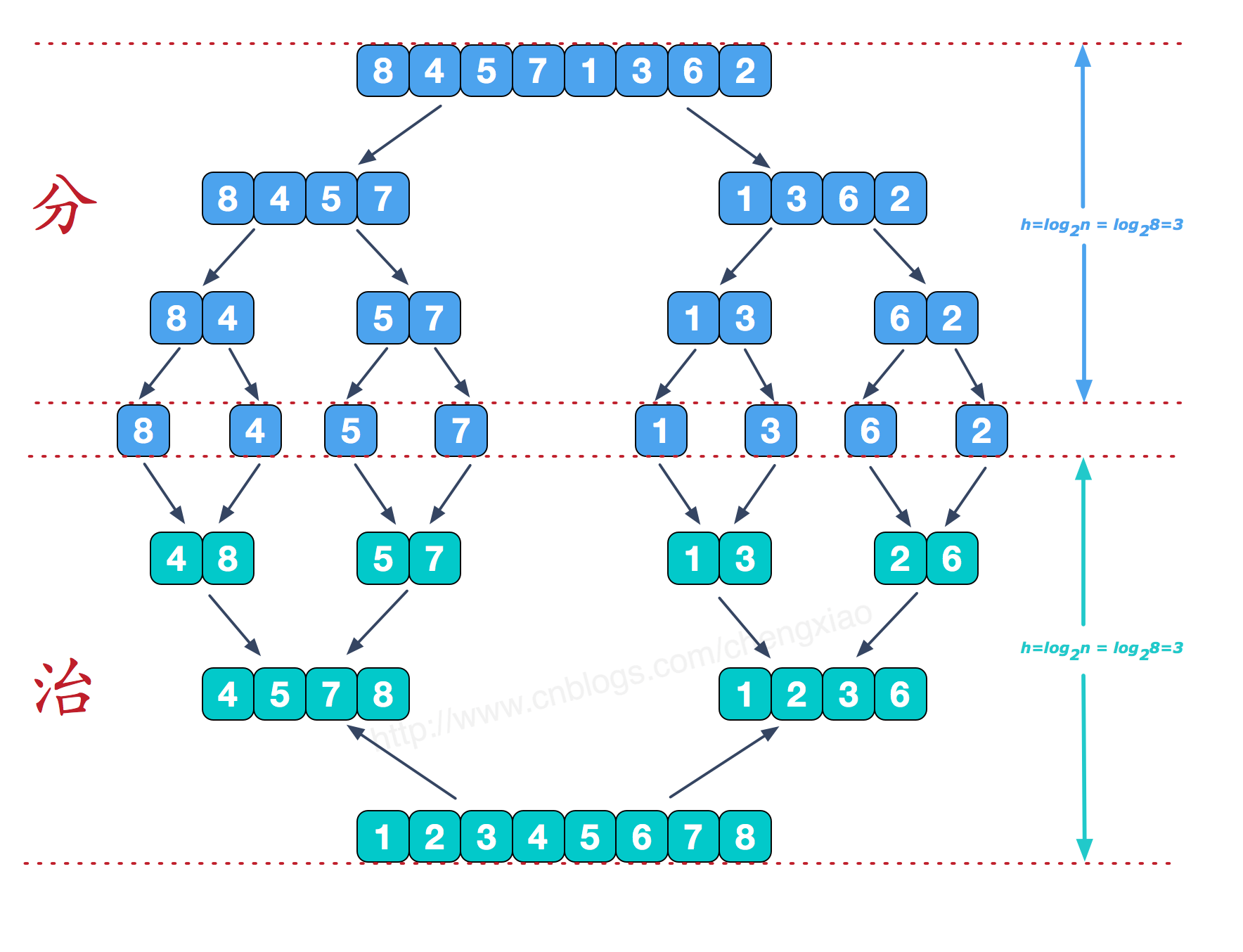
从上图可看出,“分”阶段就是递归拆分子序列的过程,递归深度为log2n。“治”的阶段则借助一个临时数组来完成,两个有序的子序列合并成一个有序序列的过程可参考下图。
代码实现
这是我实现的版本:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42public int[] mergeSort(int[] arr) {
if (arr == null || arr.length == 1) {
return arr;
}
mergeSort(arr, 0, arr.length - 1);
return arr;
}
private void mergeSort(int[] arr, int l, int r) {
if (r > l) {
int mid = (l + r) / 2;
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
sort(arr, l, mid, r);
}
}
public void sort(int[] arr, int l, int s, int r) {
int length = r - l + 1;
int[] temp = new int[length];
int i = l;
int j = s + 1;
for (int n = 0; n < length; n++) {
if (i > s && j <= r) { //全部取右边的序列
temp[n] = arr[j++];
continue;
}
if (j > r && i <= s) { //全部取左边的序列
temp[n] = arr[i++];
continue;
}
if (i <= s && j <= r) { //左右两边序列取最小的值
temp[n] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
}
}
System.out.println(Arrays.toString(temp));
for (int k = l; k <= r; k++) {
arr[k] = temp[k - l];
}
}
网上其它实现版本:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31private void mergeSortV2(int[] arr, int l, int r) {
if (l <= r) {
return;
}
//这里为什么不写成 int mid = (l + r) / 2,因为如果r值很大的话可能导致 l+r 的值溢出整型范围。
//所以严谨的写法是 int mid = l + (l + r) / 2,因为除2的操作可以用右移一位,所以也可以写成 int mid = l + (r - l) >> 2
int mid = l + (r - l) >> 1;
mergeSortV2(arr, l, mid);
mergeSortV2(arr, mid + 1, r);
sortV2(arr, l, mid, r);
}
public void sortV2(int[] arr, int l, int s, int r) {
int length = r - l + 1;
int[] temp = new int[length];
int n = 0;
int i = l;
int j = s + 1;
while (i <= s && j <= r) {
temp[n++] = arr[i] <= arr[j] ? arr[i++] : arr[j++];
}
while (i <= s) {
temp[n++] = arr[i++];
}
while (j <= r) {
temp[n++] = arr[j++];
}
for (int k = 0; k < length; k++) {
arr[l + k] = temp[k];
}
}
从上文的图中可看出,每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为logn,总的平均时间复杂度为O(nlogn)。空间复杂度则为O(n)。
归并排序是稳定排序,它也是一种十分高效的排序。java中Arrays.sort()采用了一种名为TimSort的排序算法,就是归并排序的优化版本。