排序是数据处理中十分常见且核心的操作,虽说实际项目开发中基本不需要我们手动实现,毕竟每种语言的类库中都有n多种关于排序算法的实现。但是了解这些精妙的思想对我们还是大有裨益的。本文简单介绍下最基础的三类排序算法:选择,冒泡,插入,这三种的平均时间复杂度都是O(n^2)。
先定义个交换数组元素的函数,供排序时调用:1
2
3
4
5
6
7
8
9
10
11
12/**
* 交换数组元素
*
* @param arr
* @param a
* @param b
*/
public static void swap(int[] arr, int a, int b) {
int tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
选择排序
选择排序是最简单直观的一种算法,基本思想为每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。
选择排序因为会存在元素的交换行为,属于不稳定排序。举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中两个5的相对前后顺序就被破坏了,所以是一个不稳定的排序算法。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19public int[] selectSort(int[] arr) {
if (arr == null || arr.length == 1) {
return arr;
}
int length = arr.length;
int min;
for (int i = 0; i < length - 1; i++) { //外层只需要循环 length-1 次
min = i;
for (int j = i + 1; j < length; j++) {
if (arr[j] < arr[i]) {
min = j;
}
}
if (min > i) {
swap(arr, i, min);
}
}
return arr;
}
对于上面这种选择排序,无论数组原始排列如何,比较次数是不变的,为n-1+n-2+…+1=n(n-1)/2,时间复杂度为O(n^2)。
冒泡排序
冒泡排序的基本思想是,对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或最大的元素“浮”到顶端,最终达到完全有序。
代码实现
在冒泡排序的过程中,如果某一趟执行完毕,没有做任何一次交换操作,比如数组[5,4,1,2,3],执行了两次冒泡,也就是两次外循环之后,分别将5和4调整到最终位置[1,2,3,4,5]。此时,再执行第三次循环后,一次交换都没有做,这就说明剩下的序列已经是有序的,排序操作也就可以完成了。具体代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20public int[] bubbleSort(int[] arr) {
if (arr == null || arr.length == 1) {
return arr;
}
int length = arr.length;
boolean flag;
for (int i = 0; i < length - 1; i++) {
flag = true;//设定一个标记,若为true,则表示此次循环没有进行交换,也就是待排序列已经有序,排序已然完成。
for (int j = 0; j < length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
flag = false;
}
}
if (flag) {
break;
}
}
return arr;
}
根据上面这种冒泡实现,若原数组本身就是有序的(这是最好情况),仅需n-1次比较就可完成,这种情况时间复杂度最小,为O(n);若是倒序(这是最坏的情况),比较次数为 n-1+n-2+…+1=n(n-1)/2,这是一个等差数列,其时间复杂度为O(n^2)。
插入排序
插入排序基本思想是每一步将一个待排序的数据的第一个元素,插入到前面已经排好序的有序序列中去,直到没有待排序的数据为止。。插入的时候将元素和有序序列最大值开始比较,如果小于则交换后继续与前一个值比较,直到小于等于前一个值或者到了下标为0的位置则停止,结果是有序列表中增加了一个元素,待排序列表少了一个元素。
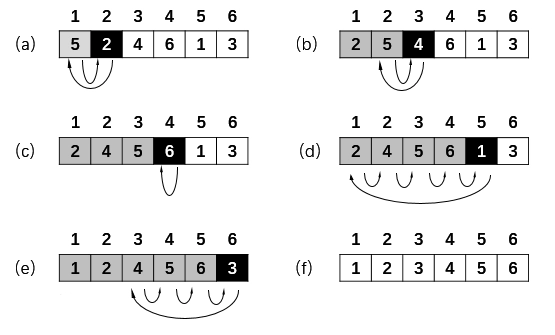
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15public int[] insertSort(int[] arr) {
if (arr == null || arr.length == 1) {
return arr;
}
int length = arr.length;
for (int i = 1; i < length; i++) {
for (int j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
swap(arr, j, j - 1);
}
}
}
return arr;
}
插入排序在已经有序的情况下(最好情况),只需要比较n-1次,无需交换元素,时间复杂度为O(n),在最坏情况下,时间复杂度依然为O(n^2)。